sistema numérico

Sistema binario de números

Un número binario sólo tiene ceros y unos.

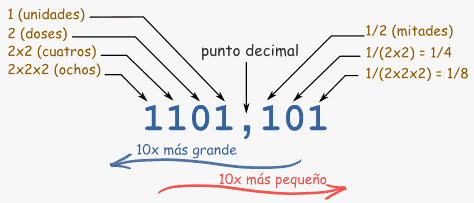Este número es 1×8 + 1×4 + 0×2 + 1 + 1×(1/2) + 0×(1/4) + 1×(1/8) (=13,625 en decimal)

De la misma manera que en el sistema decimal, se pueden poner números a la izquierda o a la derecha del punto decimal, para indicar valores mayores o menores que uno. En el sistema binario:

	El número justo a la izquierda del punto es un número entero, lo llamamos unidades. Cuando vamos a la izquierda, cada posición vale 2 veces más.
	La primera cifra a la derecha del punto significa mitades (1/2). Cuando vamos a la derecha, cada posición vale 2 veces menos(la mitad de la anterior).

Dos valores diferentes

Como sólo puedes tener ceros y unos, en binario se cuenta así:

Decimal:	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
Binario:	0	1	10	11	100	101	110	111	1000	1001	1010	1011	1100	1101	1110	1111

"El binario es tan fácil como 1, 10, 11."

Aquí tienes más equivalencias:

Decimal:	20	25	30	40	50	100	200	500
Binario:	10100	11001	11110	101000	110010	1100100	11001000	111110100

Definición de binario

	La palabra binario viene de "bi-" que significa dos. Tenemos "bi-" en otras palabras como "bicicleta" (dos ruedas) o "binoculares" (dos ojos).
	Cuando leas un número binario, pronuncia cada dígito (por ejemplo, el número binario "101" se lee "uno cero uno"). De esta manera la gente no los confunde con números decimales.

Bits

Un dígito binario por sí solo (como "0" o "1") se llama un "bit". Por ejemplo 11010 tiene cinco bits de longitud.

La palabra bit viene de las palabras inglesas "binary digit"

Cómo indicar que un número está en binario

Para mostrar que un número es binario, ponemos un pequeño 2 detrás: 101₂

De esta manera nadie pensará que es el número decimal "101" (ciento uno).

                 

Sistema de Numeración Octal

El Sistema Octal (base 8)

Representar un número en Sistema Binario puede ser bastante difícil de , así que se creó el sistema octal. En el Sistema de Numeración Octal (base 8), sólo se utilizan 8 cifras (0, 1, 2, 3, 4, 5, 6, 7)

Este Sistema de numeración una vez que se llega a la cuenta pasa a 10, etc.. La cuenta hecha en octal: 0, 1, 2, 3, 4, 5, 6, 7, 10, 11, 12, 13, 14, 15, 16, 17, 20, 21, …..  Se puede observar que en este sistema numérico no existen los números: 8 y 9.

Para pasar del un Sistema Binario al Sistema Octal se utiliza el siguiente método:

• Se divide el número binario en grupos de 3 empezando por la derecha. Si al final queda un grupo de 2 o 1 dígitos, se completa el grupo de 3 con ceros (0) al lado izquierdo.
• Se convierte cada grupo en su equivalente en el Sistema octal y se reemplaza.

        

DEFINICIÓN DEHEXADECIMAL

Hexadecimal es un adjetivo que se emplea en el ámbito de las matemáticas para aludir al sistema de numeración cuya base es el número dieciséis (16). En la actualidad este sistema suele utilizarse en la informática ya que un byte (la unidad básica de memoria) equivale a dos dígitos hexadecimales.

El sistema hexadecimal, que se abrevia Hex, apela a la notación posicional. Esto quiere decir que cada uno de sus dígitos adquiere un valor de acuerdo a su posición relativa, que se encuentra determinada por la base. Esta base, a su vez, refiere a la cantidad de dígitos que se necesitan para escribir un número.

como la base del sistema hexadecimal es dieciséis, se requieren dieciséis dígitos diferentes para la escritura. Por eso, además de los diez dígitos del sistema decimal (9, 8, 7, 6, 5, 4, 3, 2, 1 y 0), se usan las primeras seis letras del alfabeto latino: A, B, C, D, E y F.

De este modo, podemos afirmar que el conjunto de símbolos que utiliza el sistema hexadecimal está formado por los números que van del 0 al 9 y las letras de la A a la F. En este caso, A equivale 10; B, a 11; C, a 12; D, a 13; E, a 14; y F a 15.

Debido a que 2 es el único factor primo de 16, aquellas fracciones que no presentan una potencia de 2 en el denominador disponen de un desarrollo hexadecimal periódico. Por ejemplo: la fracción 1/3 en el sistema hexadecimal da como resultado 0,555555…

Así como en el sistema decimal pueden realizarse diversas operaciones, en el sistema hexadecimal también se pueden llevar a cabo distintas operaciones matemáticas. Los métodos, sin embargo, son diferentes.

Desde hace ya muchos años, en cualquier ámbito relacionado con el diseño de imagen por ordenador se utiliza el sistema hexadecimal para especificar los colores. Un código hexadecimal de color, en este marco, permite expresar los valores correspondientes a cada uno de los tres componentes al espacio escogido; por lo general se trabaja con RGB, y por lo tanto se expresa un valor para el rojo, otro para el verde y otro para el azul.

Por convención, el código suele comenzar con el signo numeral (#), tras el cual se colocan seis dígitos que pueden ir del 00 al ffo, en sistema decimal, del 0 al 255. Dicho de otra manera, en cada uno de los tres valores podemos representar hasta 256 intensidades, ya que el cero también cuenta, aunque más no sea para indicar un valor nulo.

La cantidad total de colores que podemos representar con este tipo de código hexadecimal es 16 777 216, aunque en el habla cotidiana se suele redondear hacia abajo y mencionar simplemente como «dieciséis millones de colores» o, haciendo referencia al sistema binario y usando un término más técnico, «24 bits de color» (el número 24 responde a que 2 elevado a esta potencia da como resultado exactamente 16 777 216).